排序算法

算法和数据结构的复习不写博客是不行的，之前的Algorithm项目也是进展缓慢，于是乎，我又来写博客了。准备从排序开始，把算法导论的一些算法实现下。顺便各种数据结构也要涉及下。

• 使用语言：Java
• 参考书籍：《算法导论》，《Java编程思想》

---

排序算法分类

• 比较排序。包括插入，选择，交换，归并排序等。各元素次序基于输入元素间的比较，根据决策树模型，任何比较排序在最坏情况下都要用Ω(nlgn)次比较来进行排序。
• 非比较排序，包括基数排序等。

类别	排序法	最差时间复杂度	平均时间复杂度	空间复杂度
1.插入排序	直接插入排序	O(n^2)	O(n^2)	O(1)
	希尔排序	O(n^1.3)	O(n^2)	O(1)
2.选择排序	直接选择排序	O(n^2)	O(n^2)	O(1)
	堆排序	O(nlgn)	O(nlgn)	O(1)
3.交换排序	冒泡排序	O(n^2)	O(n^2)	O(1)
	快速排序	O(n^2)	O(nlgn)	O(lgn)~O(n)
4.归并排序	归并排序	O(nlgn)	O(nlgn)	O(n) 非原地归并
5.基数排序	基数排序	O(d(r+n))	O(d(r+n)))	O(rd+n)

---

插入排序

• 基本思想：从第一个数开始，构建有序序列。对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
• 时间复杂度：O(n^2)
• 空间复杂度：O(1)
• 特点：插入排序是一个对少量元素进行排序的有效算法。

public class InsertionSort {
	public static void main(String...args){
		int[] arr = {2,52,87,62,82,62,32,96,31,69};		
		insertionSort(arr);
		System.out.println("\n插入排序后：");
		for(int i=0; i<10; i++){	
			System.out.print(arr[i] + ",");
		}
	}

	private static void insertionSort(int[] arr) {
		if(arr.length < 2) return;
		
		int firstUnsortedNum;//第一个未排序的数，我们认为arr[0]已经排好序，因而从arr[1]开始
		for(int i=1; i<arr.length; i++){
			firstUnsortedNum = arr[i];
			int j = i - 1;
			while(j>=0 && firstUnsortedNum < arr[j]){//和已排好序的数进行比较，从最后一个已排序数开始
				arr[j+1] = arr[j];
				j--;
			}
			arr[j+1] = firstUnsortedNum;
		}
	}
}

---

带二分查找的插入排序

• 基本思想：就是在插入排序中运用二分查找的方法来节约时间。在有序数组中寻找插入的位置的时候不是从后往前一个个找，而是二分查找。
• 时间复杂度：O(nlogn)
• 空间复杂度：O(n^2)
• 特点：插入排序是一个对少量元素进行排序的有效算法。

public class InsertionSort_BinarySearchEdition {
	public static void main(String...args){
		int[] arr = {2,52,87,62,82,62,32,96,31,69};		
		insertionSort(arr);
		System.out.println("\n插入排序后：");
		for(int i=0; i<10; i++){	
			System.out.print(arr[i] + ",");
		}
	}

	private static void insertionSort(int[] arr) {
		if(arr.length < 2) return;
		
		int firstUnsortedNum;
		//索引i之前的全部是已排好序的数组元素
		for(int i=1; i<arr.length; i++){
			firstUnsortedNum = arr[i];
			
			//截取字数组
			int[] sortedArr = new int[i];
			for(int m=0; m<i; m++){
				sortedArr[m] = arr[m];
			}
			
			//用二分搜索找到arr[i]应该在什么位置
			int pos = binarySearch(firstUnsortedNum, sortedArr);
			pos = Math.abs(pos);
			
			//把所有比firstUnsortedNum大的数全部右移一位
			int j = i-1;
			while(j>=pos){
				arr[j+1] = arr[j];
				j--;
			}
			arr[pos] = firstUnsortedNum;
		}
	}
	
	
	public static int binarySearch(int key, int[] list){//二分查找，返回key的索引。或者若无key，该key应该在位置（负数）
		int low = 0;
		int high = list.length - 1;
		int middle = 0;
		while(low <= high){
			middle = low + (high - low)/2;
			if(key < list[middle]) high = middle - 1;
			else if(key > list[middle]) low = middle + 1;
			else return middle;
		}
		return low*(-1);
	}
}

---

直接选择排序

• 基本思想：
  每一趟从待排序的数据元素中选出最小的一个元素，顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。
• 时间复杂度：O(n^2)
• 空间复杂度：O(1)

public class SelectSort{
	public static void main(String...args){
		int[] arr = {2,52,87,62,82,62,32,96,31,69};	
		selectSort(arr);
		
		//print the sorted array
		System.out.println("\n选择排序后：");
		for(int i=0; i<10; i++){	
			System.out.print(arr[i] + ",");
		}
	}
	
	private static void selectSort(int[] arr) {
		int i;//i代表已经排好序的个数 
		for(i=0; i<=arr.length-1; i++){
			//找到arr[i]到最后的所有数中的最小值，其索引为smallest
			int smallestIndex = i;
			for(int j =i; j<=arr.length-1; j++){
				if(arr[j] < arr[smallestIndex]){
					smallestIndex = j;
				}
			}
			//交换arr[smallestIndex]和arr[i]
			int temp = arr[smallestIndex];
			arr[smallestIndex] = arr[i];
			arr[i] = temp;
		}
	}
}

---

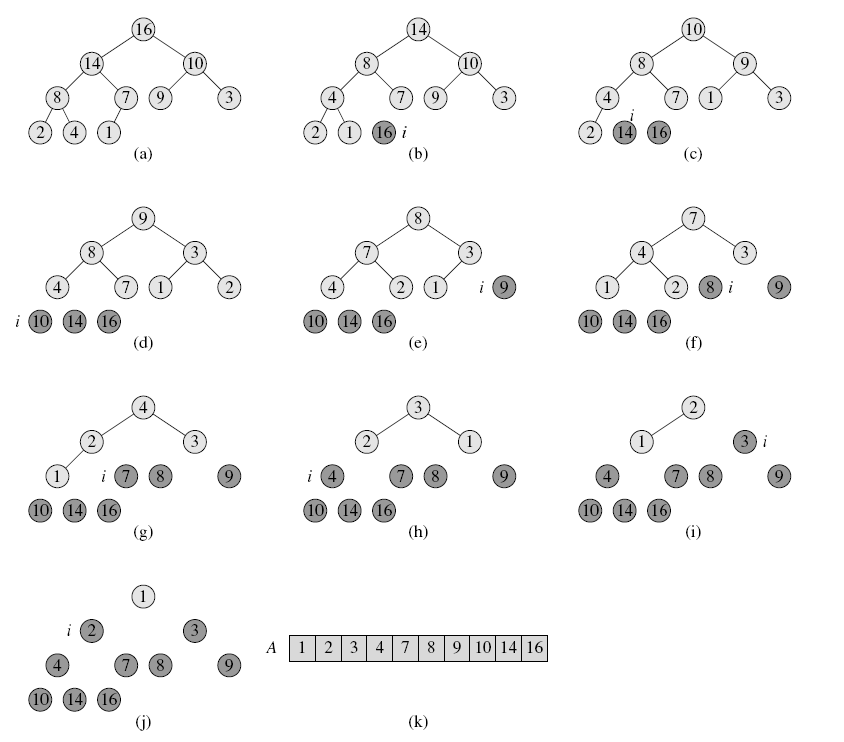
堆排序

• 基本思想：
  • 首先将数组构造成一个最大堆。
  • 因为A[0]为最大的，所以交换A[0]和A[n]，从而达到正确的位置。
  • 最后，从堆中去掉节点n（通过减小heapSize），再将A[0…n-1]建成最大堆。
• 时间复杂度：O(n^2)
• 空间复杂度：O(1)

public class HeapSort {
	public static void main(String...arg){
		int[] A = {4,1,3,2,16,9,10,14,8,7};
		heapSort(A);
		
		for(int m=0; m<A.length; m++){
			System.out.print(A[m] + ",");
		}
		System.out.println();
	}
	
	
	public static void heapSort(int[] A){
		buildMaxHeap(A);
		int heapSize = A.length;
		for(int i = A.length-1; i>0; i--){
			//exchange A[0] and A[i]
			int temp = A[0];
			A[0] = A[i];
			A[i] = temp;
			
			heapSize--;
			maxHeapify(A, 0, heapSize);

		}
	}
	
	
	//构造最大堆
	public static void buildMaxHeap(int[] A){
		int heapSize = A.length;
		int i = A.length/2 - 1;//从这里开始，A.length/2+1到最后A.length-1为叶子结点
		for(;i>=0; i--){
			//所有非叶子结点
			maxHeapify(A, i, heapSize);
		}
	}
	
	
	//当以LEFT(i),RIGHT(i)为根的两棵子树都是最大堆的时候，构造以i为根的最大堆。
	public static void maxHeapify(int[] A, int i, int heapSize){
		int left = 2 * i + 1;
		int right = 2 * i + 2;
		
		//find the largest in A[i],A[left],A[right]
		int largest = i;
		if(left < heapSize && A[left] > A[largest]){
			largest = left;
		}
		if(right < heapSize && A[right] > A[largest]){
			largest = right;
		}
		
		if(largest != i){
			//exchange A[i] and A[largest]
			int temp = A[i];
			A[i] = A[largest];
			A[largest] = temp;
			
			maxHeapify(A,largest,heapSize);
		}
	
	}
}

冒泡排序

• 算法名称：冒泡排序
• 基本思想：
  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
• 时间复杂度：O(n^2)
• 空间复杂度：O(1)

public class BubbleSort {
	public static void main(String...args){
		int[] arr = {2,52,87,62,82,62,32,96,31,69};	
		bubbleSort(arr);
		System.out.println("\n冒泡排序后：");
		for(int i=0; i<10; i++){	
			System.out.print(arr[i] + ",");
		}	
	}

	private static void bubbleSort(int[] arr) {
		if(arr.length < 2) return;
		
		int right;//每次冒泡那个最大元素落在这个索引位置上
		for(int i=0; i<arr.length-1; i++){//需要进行n-1次冒泡
			right = arr.length - 1 - i;
			for(int j=0; j<right; j++){
				if(arr[j] > arr[j+1]){
					//swap arr[j] and arr[j+1]
					int temp = arr[j];
					arr[j] = arr[j+1];
					arr[j+1] = temp;
				}
			}
		}
	}
}

归并排序

• 基本思想：
  采用分治法，将数组分成两部分，两边分别排序，然后把排好序的两个数组合并。
• 时间复杂度：O(nlogn)
• 空间复杂度：O(n)

public class MergeSort {
	public static void main(String...ages){
		int[] arr = {2,52,87,62,82,62,32,96,31,69};	
		mergeSort(arr, 0, arr.length - 1);
		System.out.println("\n排序后：");
		for(int i=0; i<10; i++){	
			System.out.print(arr[i] + ",");
		}		
	}
	
	public static void merge(int[] arr, int left, int mid, int right){
		//分成左右两个数组，左边是left,left+1,...mid
		//右边是mid+1,mid+2,...,right
		int lsize = mid - left + 1;
		int rsize = right - mid;
		int[] L = new int[lsize + 1]; //加上最后一个哨兵（最大值）
		int[] R = new int[rsize + 1];
		
		for(int i=0; i<lsize; i++){
			L[i] = arr[left + i];
		}
		L[L.length - 1] = Integer.MAX_VALUE;
		for(int j=0; j<rsize; j++){
			R[j] = arr[mid + 1 + j];
		}
		R[R.length - 1] = Integer.MAX_VALUE;
		
		int i = 0;
		int j = 0;
		for(int k = left; k<=right; k++){
			if(L[i] <= R[j]) 
				arr[k] = L[i++];			
			else
				arr[k] = R[j++];
		}	
	}
	
	public static void mergeSort(int[] arr, int left, int right){
		if(left < right){
			int mid = (left + right)/2;
			mergeSort(arr, left, mid);
			mergeSort(arr, mid + 1, right);
			merge(arr, left, mid, right);
		}
	}
	
}

---

快速排序

• 基本思想：
  1. 通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小.
  2. 再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列.
• 时间复杂度：下界为O(nlogn)，最坏情况为O(n^2)，平均时间复杂度为O(nlogn)
• 空间复杂度：在对序列的操作过程中只需花费常数级的空间，即S(1)，而在递归栈上需要花费最少logn最多n的空间

先上算法导论的图例：

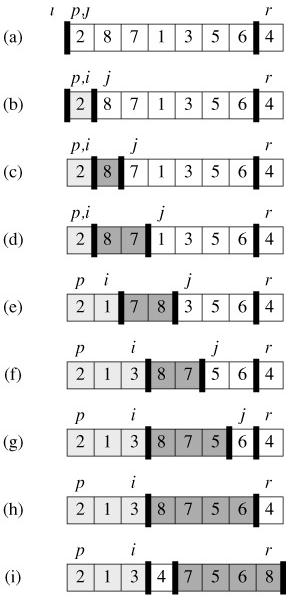
上图的伪代码如下：

QUICKSORT(A,p,r)
 		if p < r
 		  then q = PARTITION(A,p,r)  //获得主元x的索引
 		       QUICKSORT(A,p,q-1)  //对均小于x的所有数进行QUICKSORT
 		       QUICKSORT(A,q+1,r)  //对均大于x的所有数进行QUICKSORT

PARTITIONI(A,p,r)
	x = A[r]  //主元
	i = p-1   //i为已排好的数组中，小于x的最后一个
	for j = p -> r-1   //j为现在要处理的第一个
		do if A[j] <= x
			then i = i + 1
				 exchange A[i]<->A[j]   //交换第i个和第j个，让0～i均为小于x的元素
	exchange A[i+1]<->A[j]  //处理最后的主元x
	return i + 1

由于这个比较复杂，所以用python先做个简单的。

def qsort(L):
    if len(L)<=0: return L
    return qsort([x for x in L if x<L[0]]) + [x for x in L if x==L[0]] + qsort([x for x in L if x>L[0]])

L=[2, 8, 7, 1, 3, 5, 6, 4]
L=qsort(L)
print L

然后是Java版的快排。

public class QuikSort {
	public static void main(String...args){
		int[] arr = {2,52,87,62,82,62,32,96,31,69};	
		quickSort(arr, 0, arr.length - 1);
		System.out.println("\n排序后：");
		for(int i=0; i<10; i++){	
			System.out.print(arr[i] + " ");
		}			
	}
	
	public static void quickSort(int[] arr, int left, int right){
		if (left >= right) return;
		int q = partition(arr, left, right);//以arr[q]为界，递归地进行快速排序
		quickSort(arr, left, q - 1);
		quickSort(arr, q + 1, right);
	}
	
	public static int partition(int[] arr, int left, int right){
		int x = arr[right];//取最后一个数作为主元，把整个arr分成小于x和大于x的两部分
		
		int i = left - 1;//i为已排好的数组中，小于x的最后一个
		for(int j = left; j < right; j++){//j为现在要处理的第一个
			if(x >= arr[j]){
				i++;
				//exchange arr[i] and arr[j]
				//即交换当前元素和第一个大于x的元素，这样小于x的元素就都在左边0～i了
				int temp = arr[i];
				arr[i] = arr[j];
				arr[j] = temp;
			}
		}
		
		//exchange arr[i+1] and arr[r]
		int temp = arr[i+1];
		arr[i+1] = arr[right];
		arr[right] = temp;
		
		return i+1;
	}
}